Texas Instruments (TI) Calculator for Finance Problems

You may use any of these TI calculators:
TI-83 Plus
TI-84 Plus series
TI-Nspire CX series
TI-89 Titanium
TI-73 Explorer

There are at least two approaches to using the TI-calculators for finance problems.
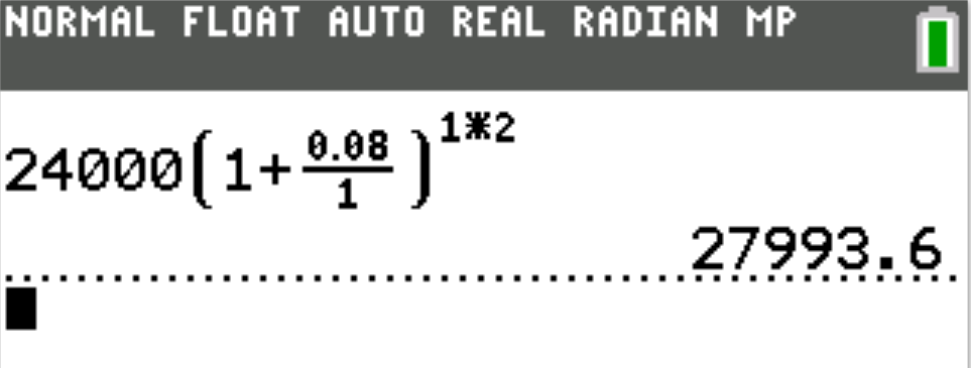
1st Approach: Direct Input of Substituted Values
(1.) Find the applicable Formula
(2.) Substitute the values directly in the formula.
(3.) Enter it directly in the calculator.
(Please see Show/Hide Answer for examples.)

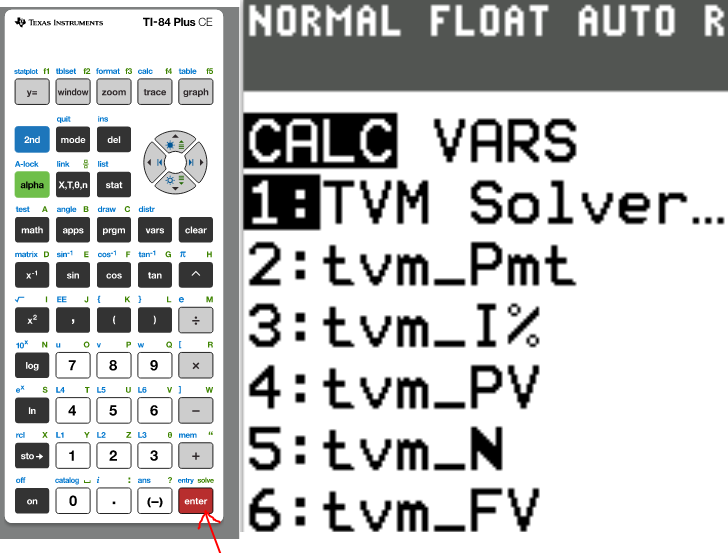
2nd Approach: Time Value of Money (TVM) Solver
The Finance app is required.
It can be assessed by pressing the APPS button, then pressing the 1: Finance app
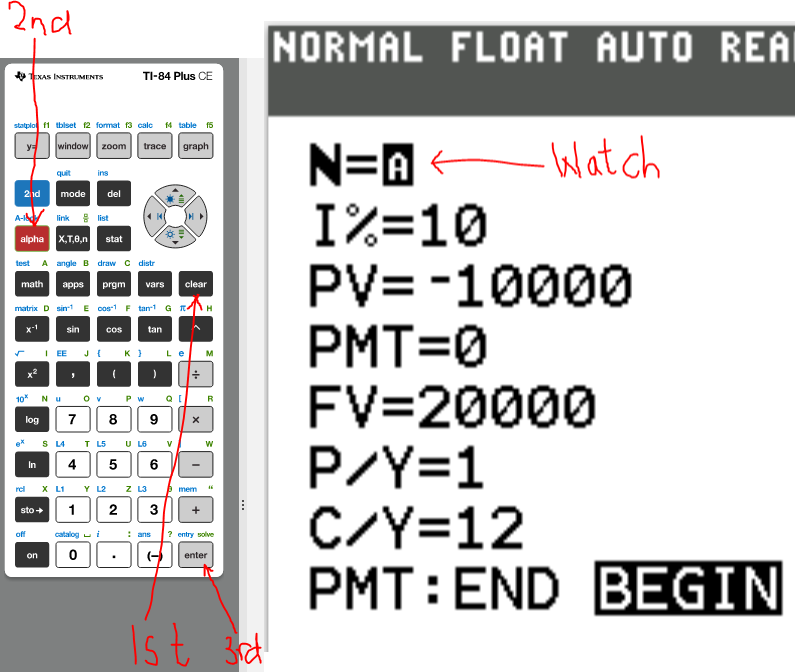
We begin with the TVM Solver (known as the Time Value of Money Solver) which is found as the first app under the CALC menu (CALC → 1: TVM Solver ...)

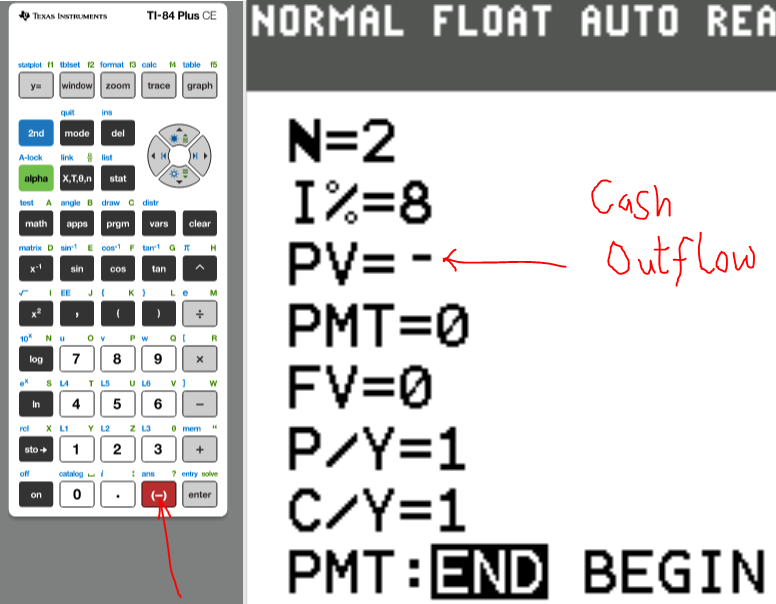
N is the total number of compounding periods (years). $N = mt$
I% is the interest rate. If it is 3%, type 3. Do not include the %.
PV is the present value.
PMT is the periodic payment.
FV is the future value.
P/Y is the number of payments per year.
C/Y is the number of compounding periods per year.
PMT:END:BEGIN Is the payment made at the end or at the beginning of the year?

Notable Notes:
(1.) No field should be blank.
Put a value in every field.
For the value you would like to find, put 0 initially.

(2.) For any cash outflow, put a negative sign.
For any cash inflow, put a positive sign.

(3.) Indicate whether the payment is made at the END or at the BEGIN of a period.
When the black focus is on any of those options, move to the field that you want to calculate.

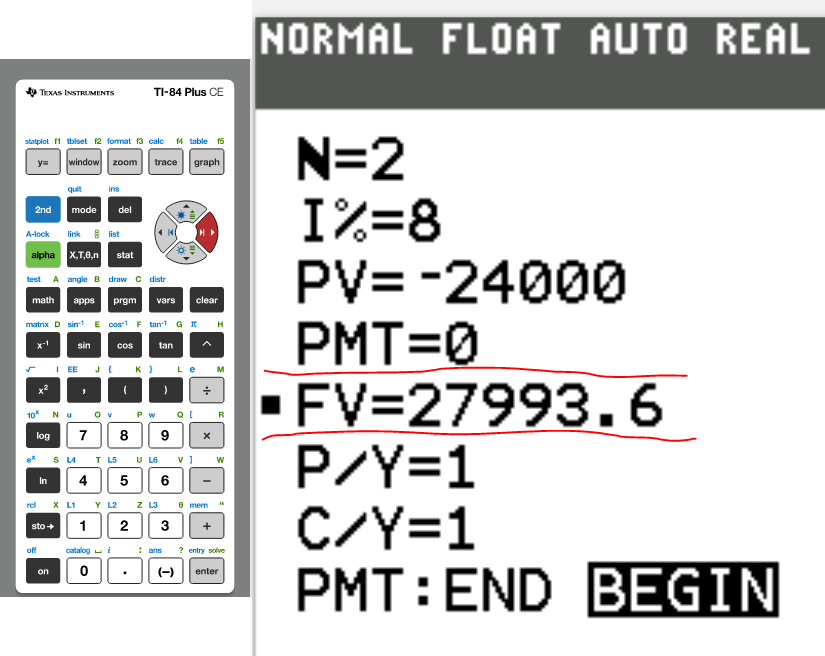
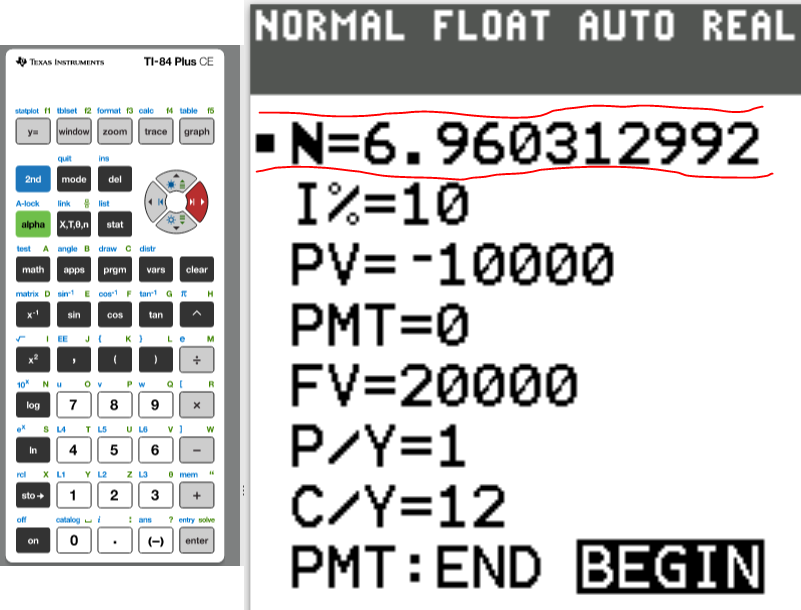
(4.) Clear the 0 that you put in initially in that field.
Press the ALPHA key
That takes us to the SOLVE menu which is above the ENTER key. So, press the ENTER key.
That gives the value of what you want to calculate.

Let us do some examples.
NOTE: Please begin from the first example. Do not skip.

Compound Interest Application
(1.) CSEC A credit union pays 8% per annum compound interest on all fixed deposits.
A customer deposited $24,000 in an account.
Calculate the TOTAL amount of money in the account at the end of two years.

Show/Hide Answer

$ r = 8\% = \dfrac{8}{100} = 0.08 \\[5ex] P = \$24000 \\[3ex] A = ? \\[3ex] t = 2\:years \\[3ex] Compounded\:\:per\:\:annum \implies m = 1 \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = P\left(1 + \dfrac{0.08}{1}\right)^{1(2)} \\[5ex] A = 24000(1 + 0.08)^2 \\[4ex] A = 24000(1.08)^2 \\[4ex] A = 24000(1.1664) \\[3ex] A = 27993.6 \\[3ex] $ The total amount of money in the account at the end of two years is $\$27,993.60$

The right arrows are for directional purposes.
24000 → (→ 1 → + → MATH → ⟩⟩⟩⟩ FRAC → 1:n/d → $\dfrac{0.08}{1}$ →) → $^$ → 1 * 2 ⟩ ENTER

Compound Interest Application
(2.) How long will it take an investment of $10,000 to double if the investment earns interest at the rate of 10% per year compounded monthly?

Show/Hide Answer

$ P = \$10000 \\[3ex] A = double\:\:P = 2(10000) = \$20000 \\[3ex] r = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] Compounded\:\:Monthly \implies m = 12 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] \dfrac{A}{P} = \dfrac{20000}{10000} = 2 \\[5ex] \dfrac{r}{m} = \dfrac{0.1}{12} = 0.0083333 \\[5ex] t = \dfrac{\log 2}{12 * \log(1 + 0.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * \log(1.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * 0.003604124} \\[5ex] t = \dfrac{0.301029995}{0.043249491} \\[5ex] t = 6.96031301 \\[3ex] t \approx 6.96 \\[3ex] $ It will take about $6.96\:years$ for the investment of $\$10,000$ to double at the rate of $10\%$ per year compounded monthly

The right arrows are for directional purposes.
Numerator:
MATH → ⟩⟩⟩⟩ FRAC → 1:n/d → $\log \left(\dfrac{2000}{10000}\right)$
Denominator:
12 → $\log$ (→ 1 → + → MATH → ⟩⟩⟩⟩ FRAC → 1:n/d → $\dfrac{0.1}{12}$)
⟩ ENTER

Future Value of Ordinary Annuity Application
(3.) Determine the savings plan balance after 15 months with an APR of 2% and monthly payments of $300

Show/Hide Answer

$ PMT = \$300 \\[3ex] r = 2\% = \dfrac{2}{100} = 0.02 \\[5ex] Monthly\;\;payments \rightarrow Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 15\;months = \dfrac{15}{12} = 1.25\;years \\[5ex] FV = ? \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 12 * 300 * \left[\dfrac{\left(1 + \dfrac{0.02}{12}\right)^{12 * 1.25} - 1}{0.02}\right] \\[10ex] = 3600 * \left[\dfrac{\left(1 + 0.001666667\right)^{15} - 1}{0.02}\right] \\[10ex] = 3600 * \left[\dfrac{\left(1.001666667\right)^{15} - 1}{0.02}\right] \\[7ex] = 3600 * \left[\dfrac{1.025293784 - 1}{0.02}\right] \\[5ex] = 68400 * \left[\dfrac{0.025293784}{0.02}\right] \\[5ex] = \dfrac{3600 * 0.025293784}{0.02} \\[5ex] = \dfrac{91.05762139}{0.02} \\[5ex] = 4552.881069 \\[3ex] FV \approx \$4,552.88 \\[3ex] $