(7.) The Luke's family just closed on a 15-year mortgage home for
120,000 at 7% per annum.
Angel Bank is financing the home.
for the mortgage.
This is a case of
Amortization
$
PV = \$120000 \\[3ex]
t = 15\: years \\[3ex]
r = 7\% = \dfrac{7}{100} = 0.07 \\[5ex]
Compounded\:\:monthly \rightarrow m = 12 \\[3ex]
PMT = ? \\[3ex]
PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex]
PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex]
PMT = \dfrac{120000}{12} * \left[\dfrac{0.07}{1 - \left(1 + \dfrac{0.07}{12}\right)^{-1 * 12 * 15}}\right] \\[10ex]
= 10000 * \left[\dfrac{0.07}{1 - \left(1 + 0.00583333333\right)^{-180}}\right] \\[7ex]
= 10000 * \left[\dfrac{0.07}{1 - \left(1.00583333333\right)^{-180}}\right] \\[7ex]
= 10000 * \left[\dfrac{0.07}{1 - 0.351006914}\right] \\[5ex]
= 10000 * \left[\dfrac{0.07}{0.648993086}\right] \\[5ex]
= \dfrac{10000 * 0.07}{0.648993086} \\[5ex]
= \dfrac{700}{0.648993086} \\[5ex]
= 1078.59393 \\[3ex]
PMT \approx \$1078.59\\[3ex]
Number\:\:of\:\:payments = m * t \\[3ex]
Number\:\:of\:\:payments = 12 * 15 = 180\:payments \\[3ex]
$
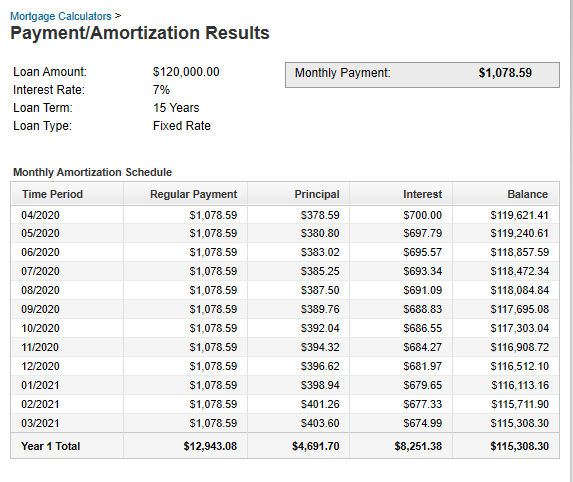
| Loan Amortization Schedule for the Luke's Family |
Annual $\%$Rate: $7\%$
Amount of Mortgage: $\$120,000$
Number of Monthly Payments: $180$
|
Monthly Payment: $\$1,078.59$
Term: Years $15$, Months $0$
|
| Payment Number |
Interest Payment |
Principal Payment |
Balance of Loan |
| $1$ |
$\$700.00$ |
$\$378.59$ |
$\$119,621.41$ |
| $2$ |
$\$697.79$ |
$\$380.80$ |
$\$119,240.61$ |
| Complete it |
Complete it |
Complete it |
Complete it |
$
\underline{Payment\:\:Number\:1} \\[3ex]
Interest\:\:Payment = P * r * t = 120000 * 0.07 * \dfrac{1}{12} = \$700.00 \\[5ex]
Principal\:\:Payment = Monthly\:\:Payment - Interest\:\:Payment \\[3ex]
Principal\:\:Payment = 1078.59 - 700.00 = \$378.59 \\[3ex]
Balance\:\:of\:\:Loan = Principal\:\:Balance - Principal\:\:Payment \\[3ex]
Balance\:\:of\:\:Loan = 120000.00 - 378.59 = \$119621.41 \\[3ex]
$
NOTE: For the first payment:
The Principal Balance is the Amount of Mortgage
The Principal is also the Amount of Mortgage.
For the second payment:
The Principal Balance is the Principal for the second payment.
The Principal Balance is also the Balance of Loan after the first payment.
For the third payment:
The Principal Balance is the Principal for the third payment.
The Principal Balance is also the Balance of Loan after the second payment.
...and so on...and so forth...
$
\underline{Payment\:\:Number\:2} \\[3ex]
Interest\:\:Payment = P * r * t = 11962.41 * 0.07 * \dfrac{1}{12} = \$697.79 \\[5ex]
Principal\:\:Payment = Monthly\:\:Payment - Interest\:\:Payment \\[3ex]
Principal\:\:Payment = 1078.59 - 697.79 = \$380.80 \\[3ex]
Balance\:\:of\:\:Loan = Principal\:\:Balance - Principal\:\:Payment \\[3ex]
Balance\:\:of\:\:Loan = 119621.41 - 380.80 = \$119240.61 \\[3ex]
$
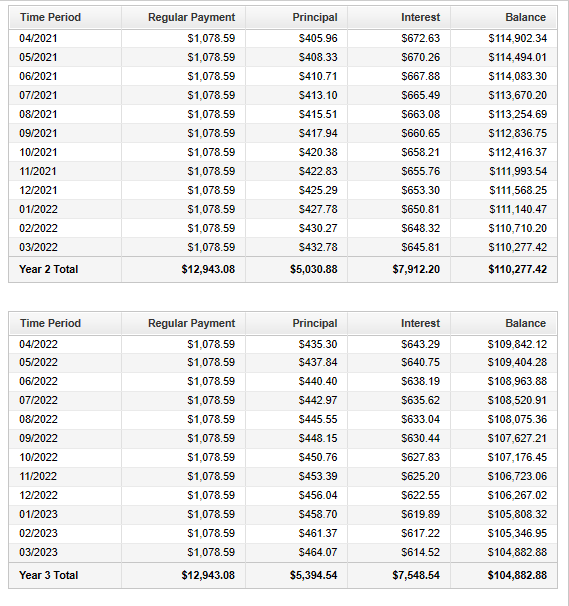
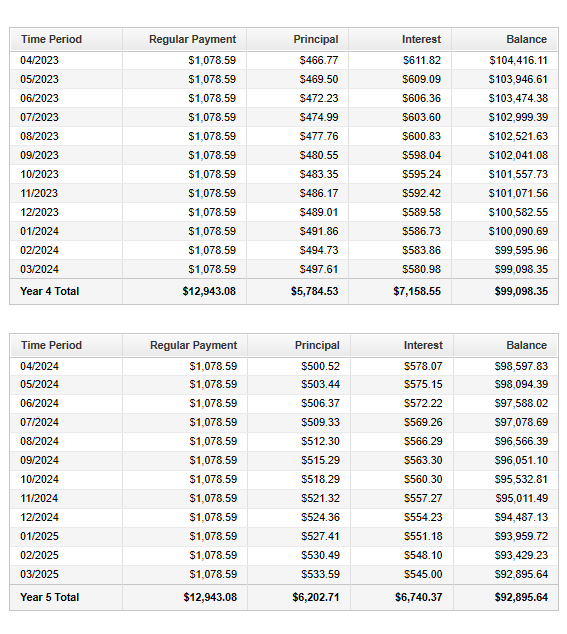
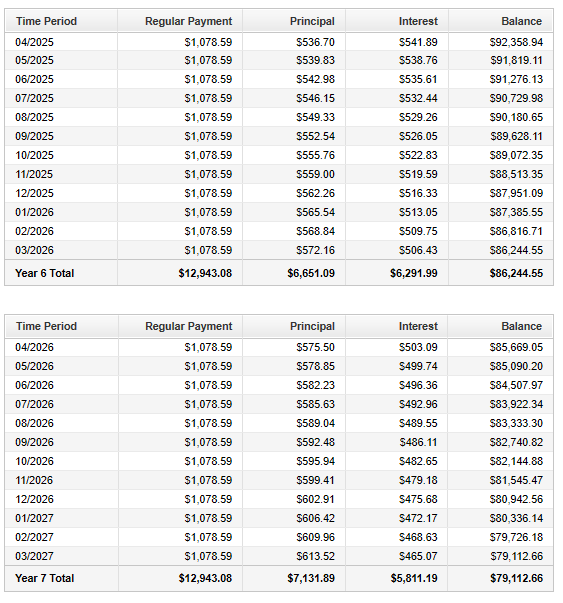
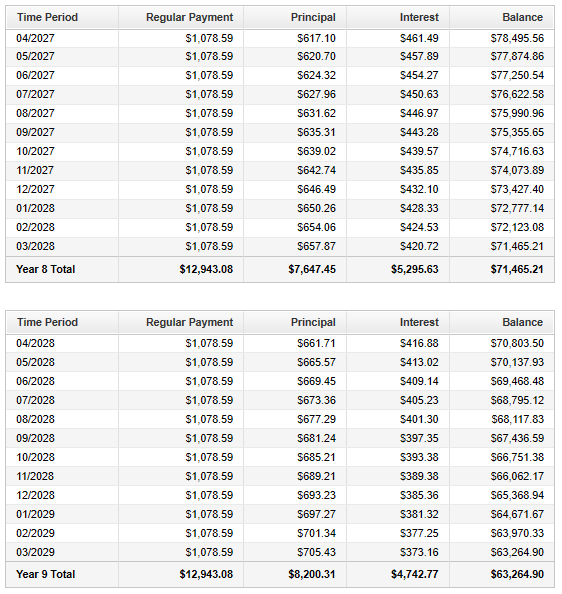
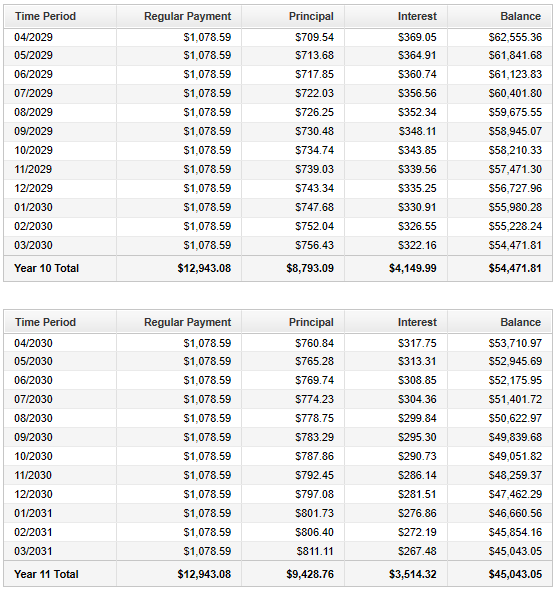
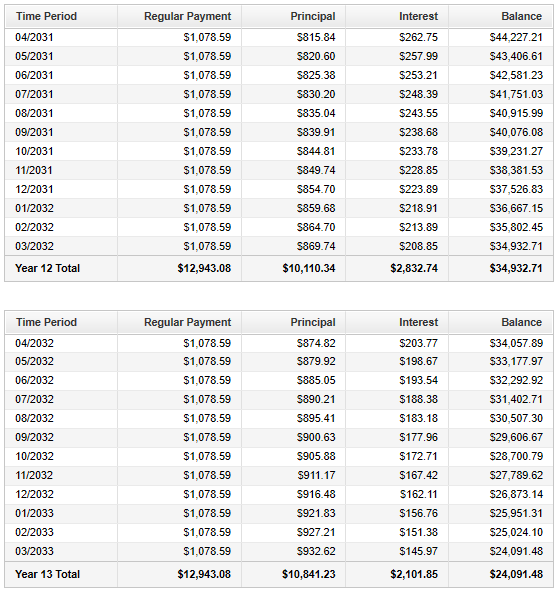
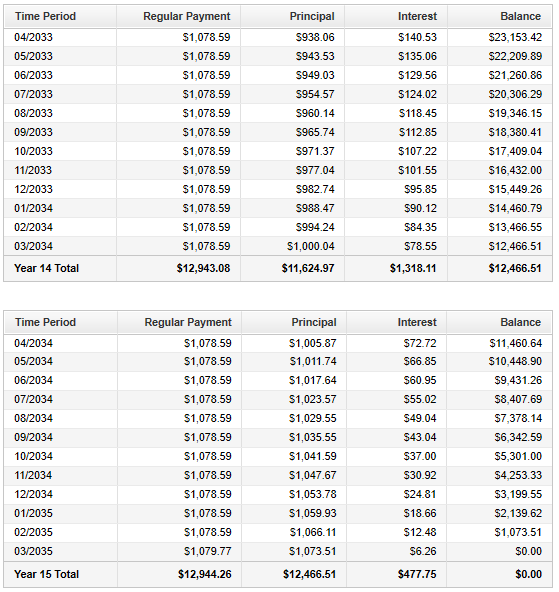
Complete the rest of the Loan Amortization Table.
Check your answers with the calculator (please see the top page)
You can also check your answers using the table below.
 Formulas Used: Mathematics of Finance
Formulas Used: Mathematics of Finance